Newton's Method for Finding Roots

5.1 Newton's Method for Finding Roots

We are going to learn about Java by studying the example program which calculates the roots of a function using Newton's method. Before you dig too deeply into the code, though, you should familiarize yourself with what Newton's method does.

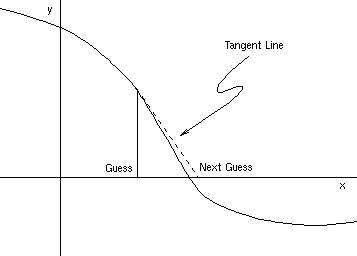
The idea behind Newton's method is that a differentiable function can be approximated locally by a straight line. So if you know the approximate location of a root, you should be able to get a better estimate for the root by solving the linear equation that approximates the function. A diagram should help here.

The mathematics behind the heuristics are pretty easy. If we have a function f and a guess for a root at x0 then our approximation for the function is:

f(x) = f(x0) + f'(x0)(x - x 0)
Since we are solving for f(x)=0, we can substitute this into the equation and solve for x to get:
x = x0 - f(x0)/f'(x0)
We can then iterate this procedure with the hopes of narrowing in on the correct root. Our example will be a program that takes an inital guess and produces a result for a root of sin. Here is how the code will look like when you run it with an inital guess of 2: 

(maxwell@gamba.130) java Newton 2
Step: 1 x:4.18504 Value:-0.864144
Step: 2 x:2.46789 Value:0.623881
Step: 3 x:3.26619 Value:-0.124272
Step: 4 x:3.14094 Value:0.000648741
Step: 5 x:3.14159 Value:-9.10111e-11
Zero found at x=3.14159
(maxwell@gamba.131)
Next, lets look at the Java code that produced this output.
Next 5.2 Java Code for Newton's Method
David Maxwell, who is still writing this, would like to hear your comments and suggestions.